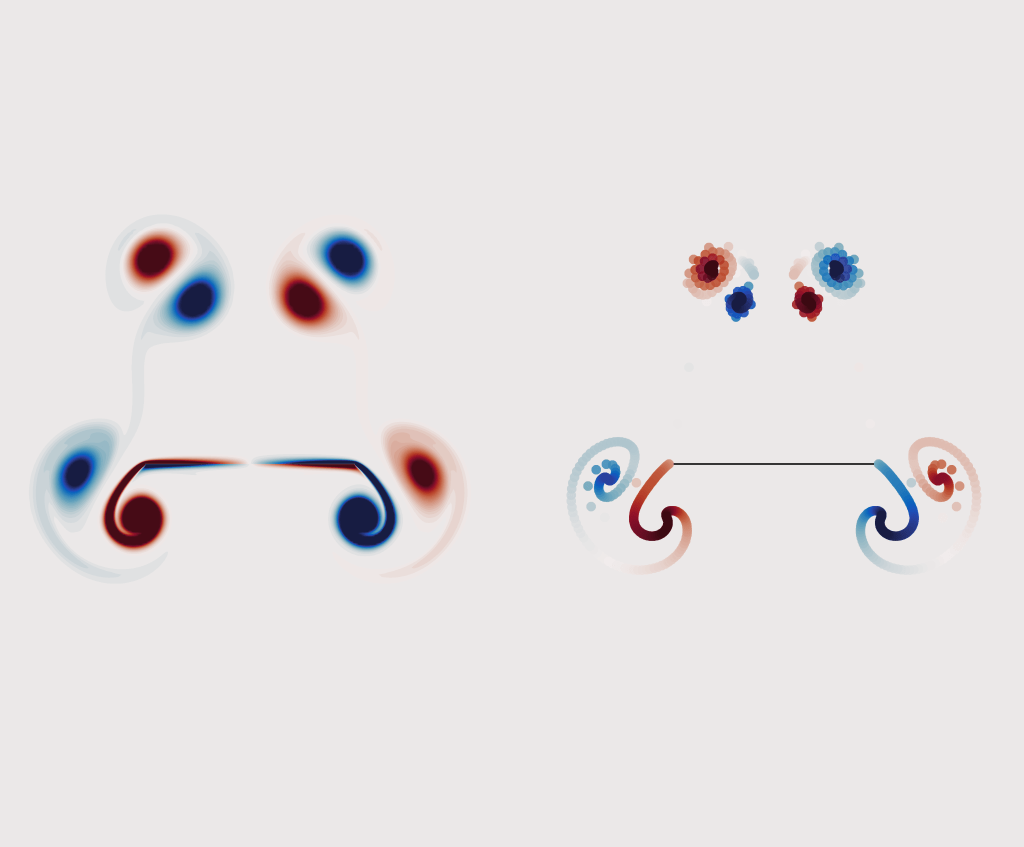I develop fast, stable, and mathematically grounded physics-based simulation algorithms. I’m generally interested in problems related to bio-locomotion as well as more fundamental problems related to numerical and complex analysis (much of what I do is secretly about the theory and computation of singular integral equations). Here are some of the things I’ve thought about!
Preprints
Inviscid vortex sheet models provide fast, reduced-order descriptions of fluid–structure interaction by compressing the vorticity into a thin, lower-dimensional interface. For over a century, such models have been used to study unsteady aerodynamic phenomena. Yet their quantitative accuracy relative to the real viscous flows they seek to model has remained uncertain. Here we present a broad and uniform comparison between a single vortex sheet formulation and direct Navier–Stokes simulations across a large collection of plate maneuvers.
By enforcing consistent zero-thickness geometry and carefully resolving numerical singularities in both viscous and inviscid computations, we identify the regimes in which inviscid models accurately reproduce vortex dynamics and force histories, as well as those in which viscous effects are essential. Across most motions considered, the inviscid model achieves 10–20% average relative error. These results clarify the practical limits of inviscid modeling and support its use for the rapid exploration and control of complex unsteady flows.
I’ll be giving a talk about this at the 20th U.S. National Congress of Theoretical and Applied Mechanics.
Publications
Fluid Dynamics and Numerical Analysis
- Falling plates with leading-edge vortex shedding
(“Editors’ Suggestion”, Phys. Rev. Fluids)
We developed a new vortex shedding model for falling thin objects (eg. leaves, wings) that captures the essential physics of these systems by incorporating leading edge shedding. Despite its simplicity, the model accurately predicts the transition point in density where fluttering transitions to tumbling. Here are some neat videos! The blue and orange are the vortex sheets, and capture the clockwise and anti-clockwise “spin” (called vorticity) at that spot. As the plate moves through the fluid, it injects angular momentum into it from its two edges, “dyeing” it blue and orange.
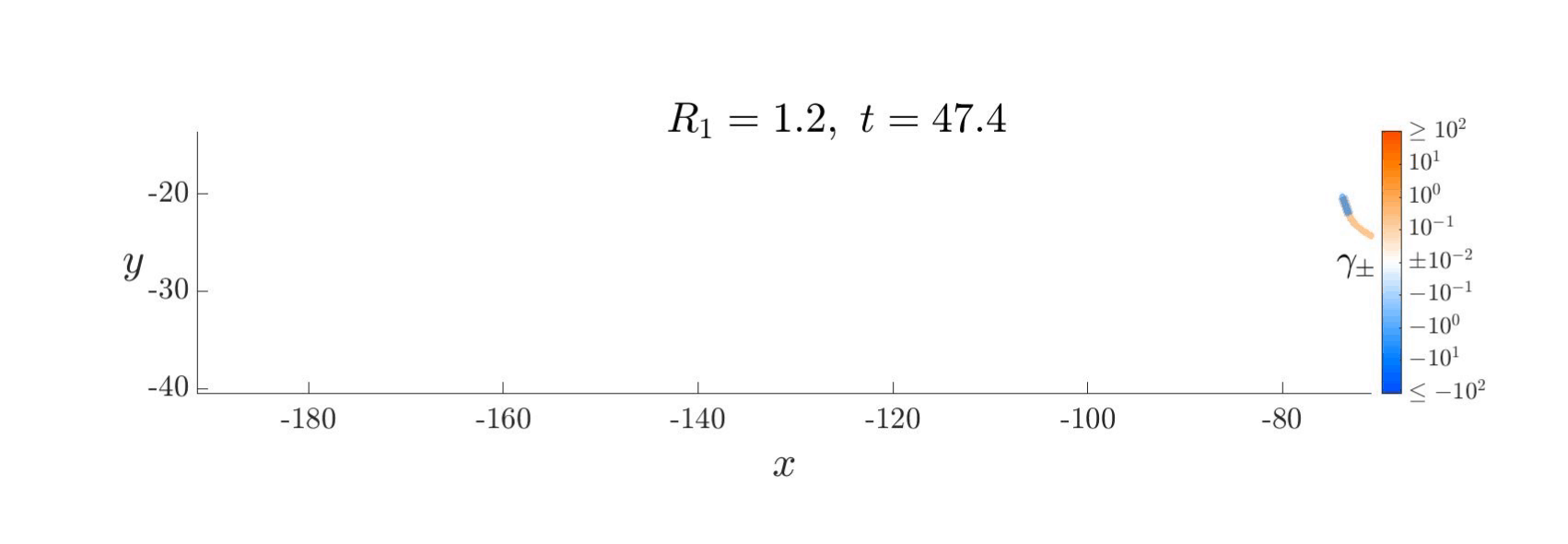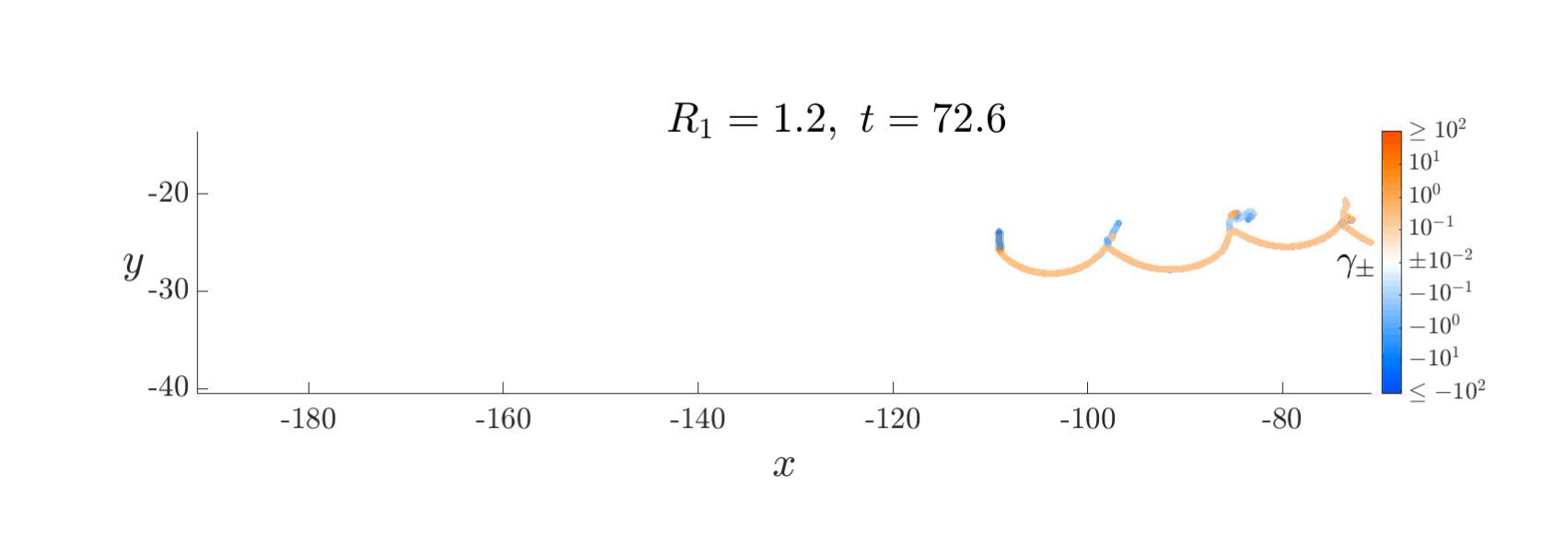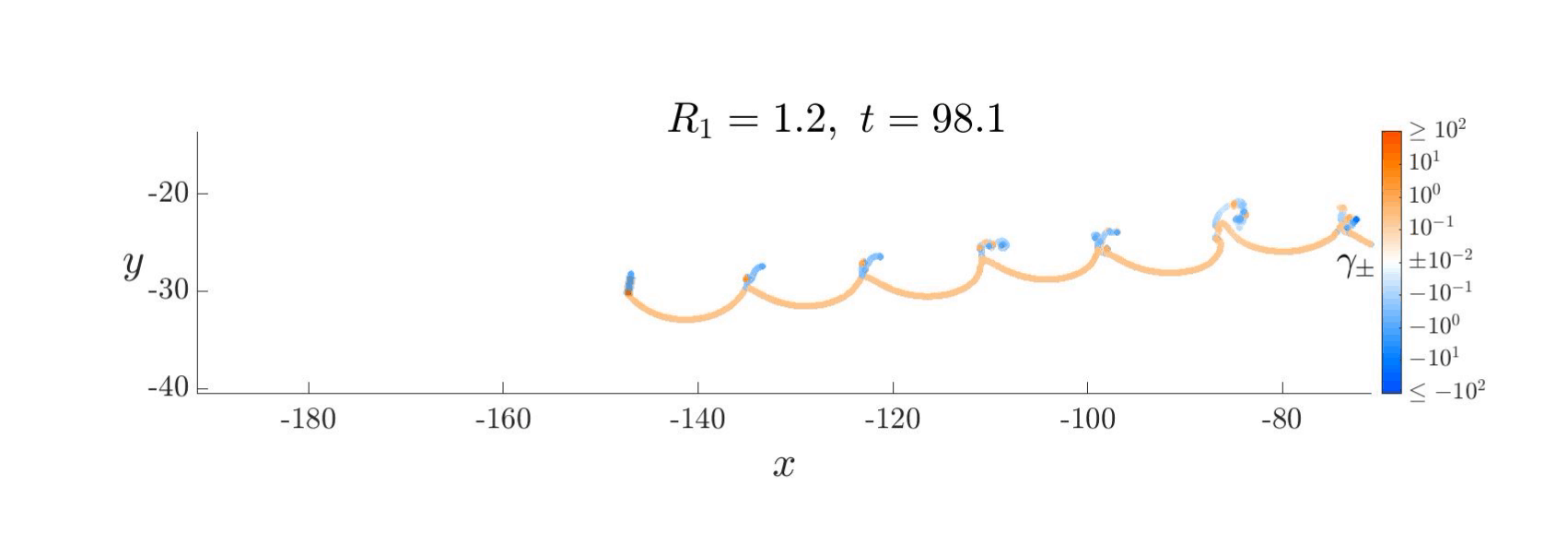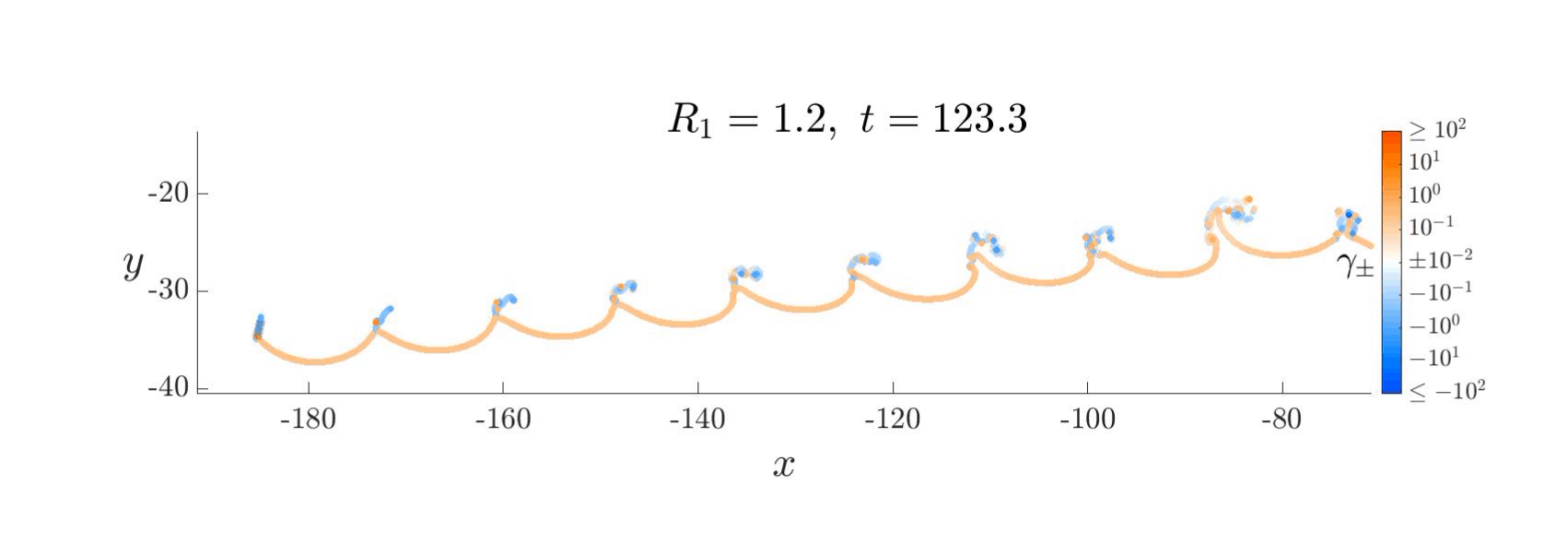
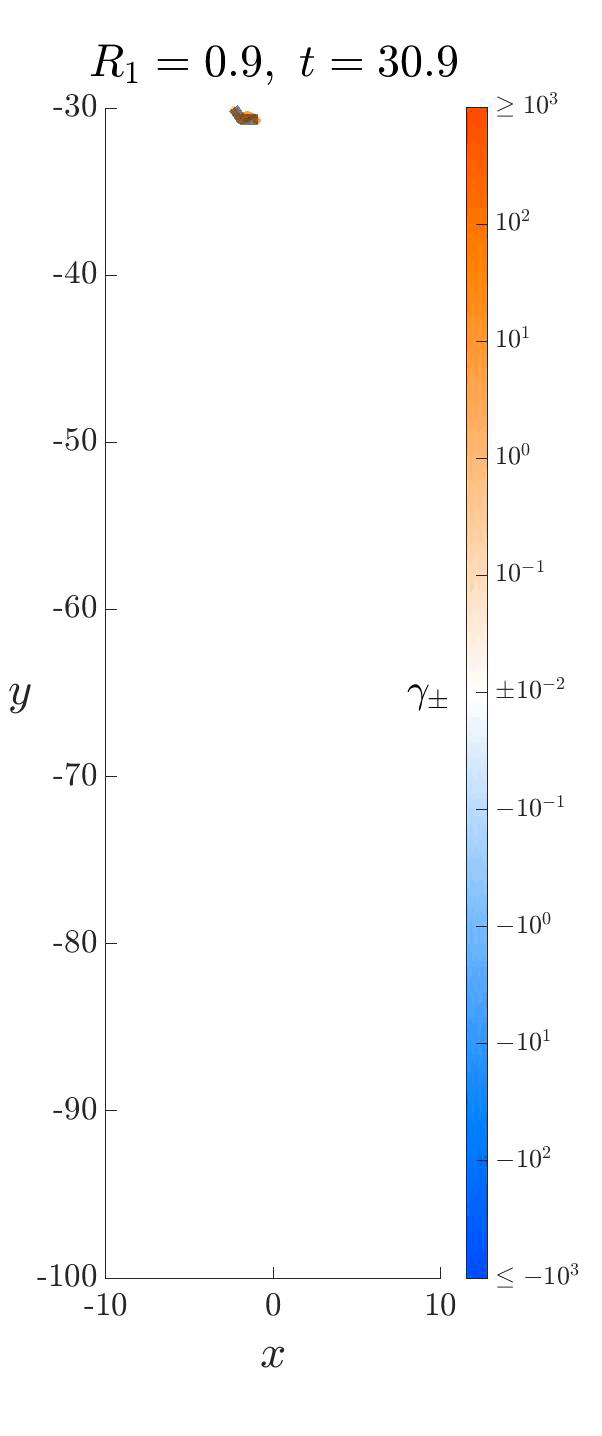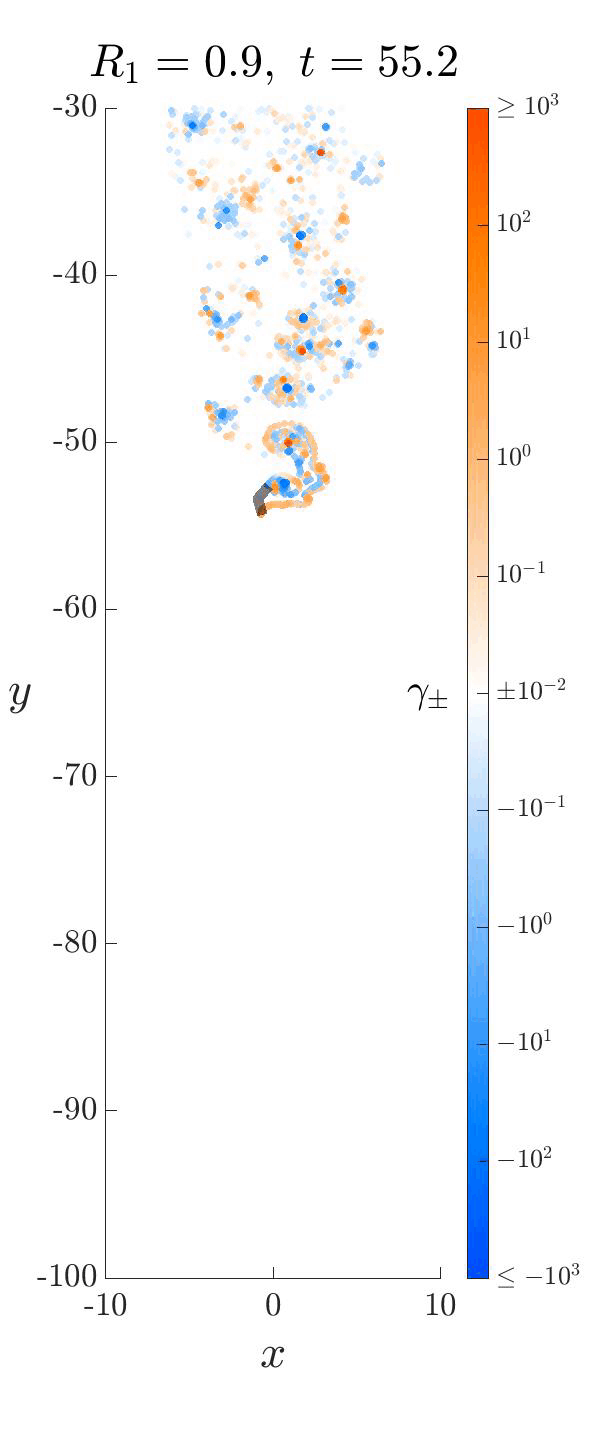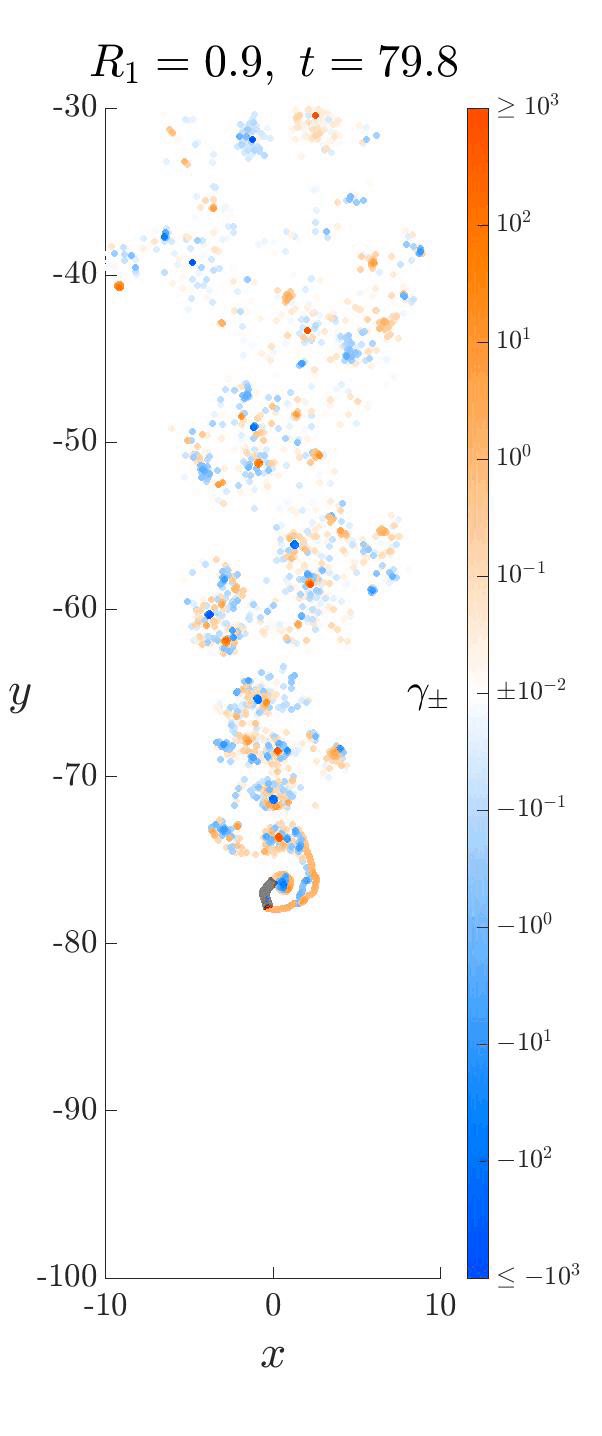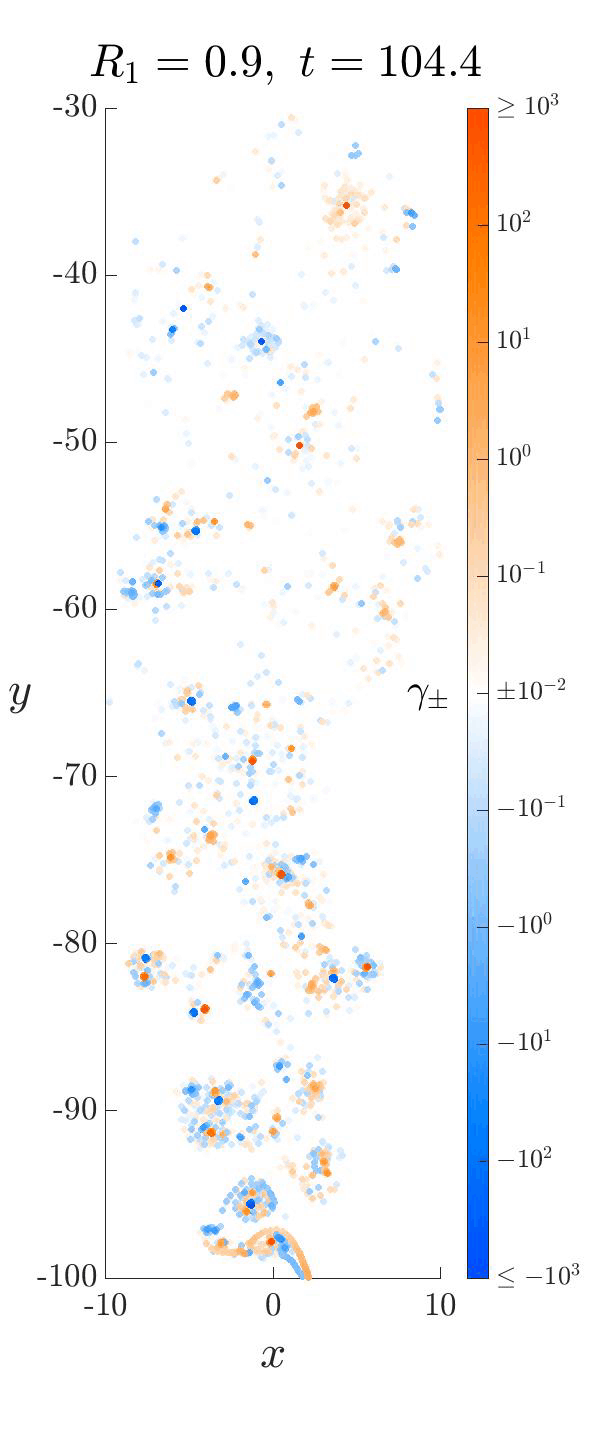
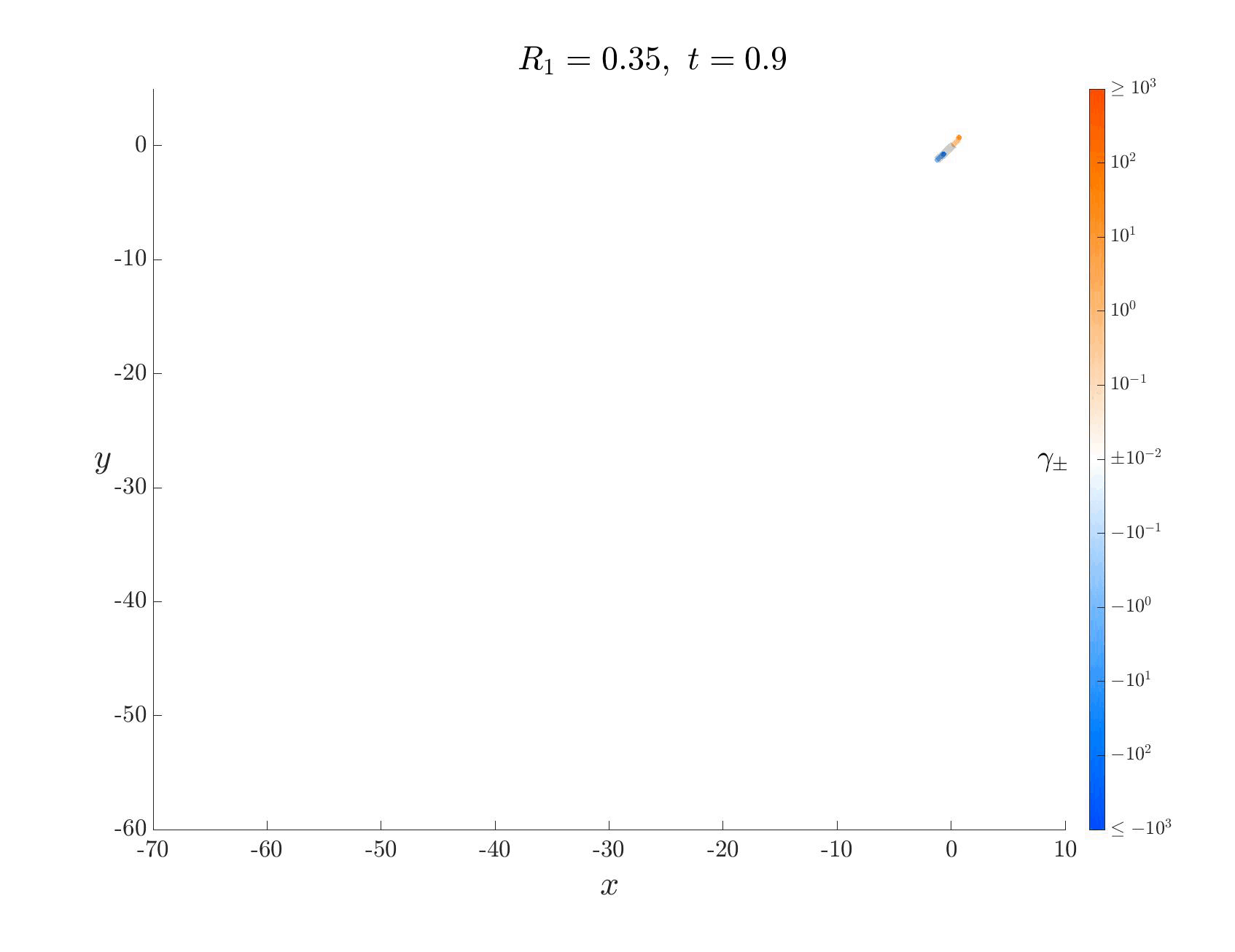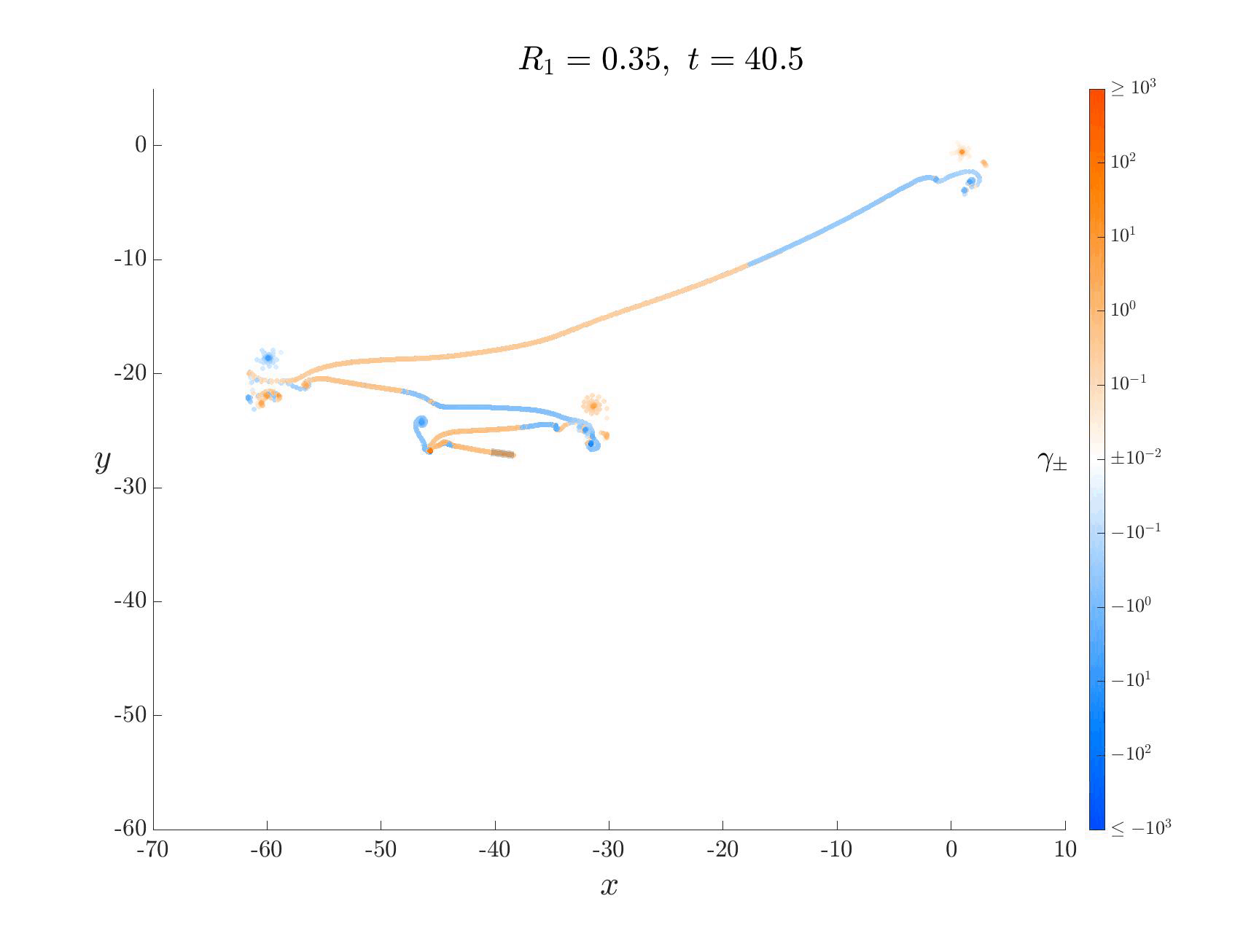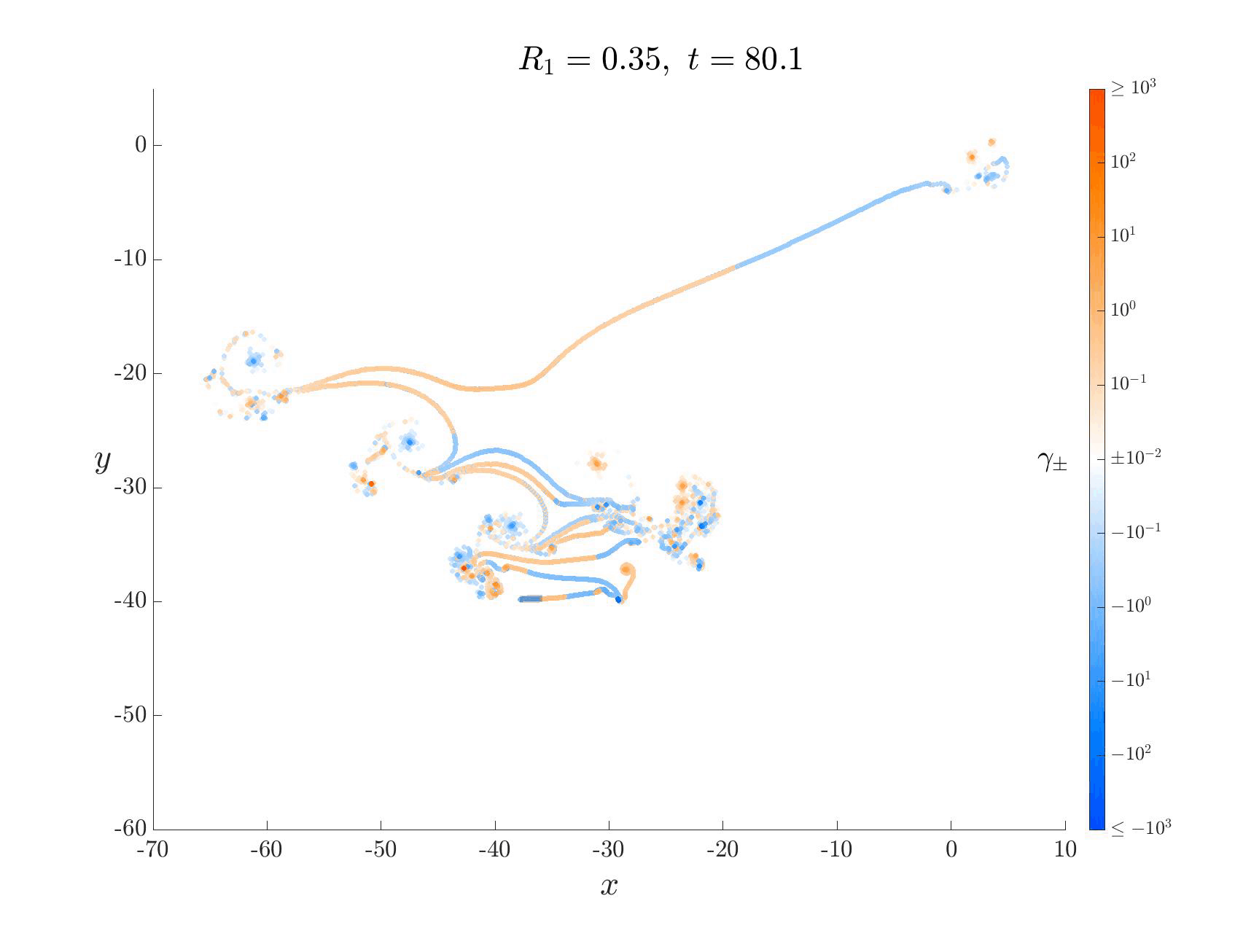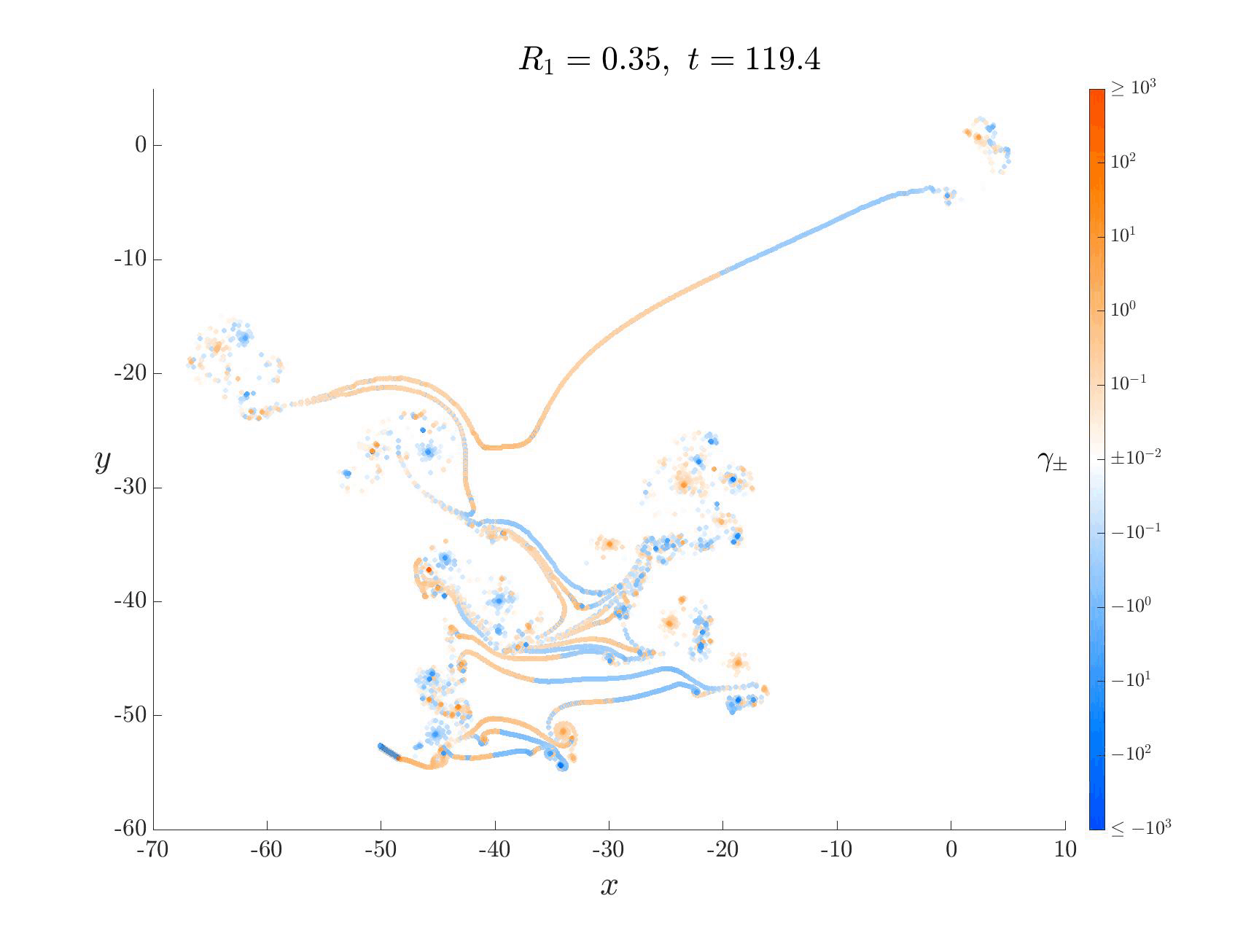
Each of these falling modes resemble different motions that can be observed in nature. For example, one can imagine birds exploiting the passive dynamics of the large amplitude fluttering motion above to efficiently glide from treetop to treetop with minimal effort.
I gave a talk about this at DisCoVor 2025. Here are the slides!
Complex Analysis
We prove optimal Hölder regularity for a canonical solution operator to the
A key observation is that the unique solution operator whose Cauchy integral over the Shilov boundary of the polydisc (the torus) vanishes actually preserves Hölder regularity. As it turns out, this canonical operator appears in several classical guises in the literature, including the Henkin formula and the Nijenhuis–Woolf formula. By combining these seemingly different representations, we establish optimal Hölder regularity for the underlying canonical solution operator.
While our proof is carried out on the polydisc, the method extends to general product domains, though the required estimates become substantially more technical.
Loo Yu Jun 